Email:
yoginder@iisc.ac.in
Address:
#409, SERC
Indian Institute of Science (IISc)
Bangalore-560012.
Karnataka, India.
Phone:
+91-80-2360 0492 (Extn. 409)
+91-80-2293 2899
- Computational Electromagnetics. With the use of high-frequency electromagnetic bands and the increased complexity of electromagnetic and Radio Frequency (RF) devices, the design/analysis time cycle and cost of electromagnetic devices have increased tremendously. The design cycle cost and time can be reduced by using numerical modeling tools, and Computational Electromagnetics (CEM) is a vital part of developing various electromagnetics design/analysis tools. These tools can solve radiation/scattering problems for antenna, Electromagnetic Interference (EMI)/ Electromagnetic Compatibility (EMC) problems, and Radar Cross Section (RCS) analysis. CEM methods can broadly divide into differential equations, i.e., Finite Element Method (FEM), Finite Difference Time Domain Method (FDTD), and frequency domain method, i.e., Method of Moment (MoM) or Boundary Element Method (BEM). The main goal of all these methods is to enable the electromagnetics community to analyze and design RF devices with computer models. The accuracy, solving time, and system memory requirement are critical factors for solving EM problems using various CEM methods. Last few decades CEM community has overcome some of the challenges. However, solving multi-scale and significant electric wavelength size EM problems accurately and efficiently is still tricky.
- Fast Hierarchical Matrix (H-Matrix) solvers. A surface or volume mesh in MoM solvers gives rise to a smaller matrix size than the FEM-based solvers, but the matrix computed is in dense form, presenting a fill time, solution time, and high matrix storage memory bottleneck. Several fast iterative solver algorithms have been proposed to mitigate the problem: the Fast Multipole Method (FMM) and low-rank matrix compression methods like H-Matrix are a few of them. Algebraic fast solvers like H-Matrix are more popular than fast analytic solvers like FMM due to the ease of implementation and kernel independence property. While these algorithms can reduce the cost of matrix-vector products to O(N) or O(NlogN), the solution time depends on the convergence rate of the iterative solution. Also, as the number of unknowns increases, the solution iteration count increases, increasing the solution time. The solution time can be accelerated using a matrix preconditioner in the iterative solution process. Developing a kernel-independent and stable pre-conditioning matrix, particularly for full-wave applications, is challenging in CEM.
- High Performance Computing. In recent decades, there has been substantial growth in the use of large scale modeling, simulation umang CEM community to devise solutions for complex problems and to push innovation forward. These simulations are limited by the transistor desity in microprocessor due to the processor heat dessipation, this has given rise to the many-core CPU architectures that rely on increasing the number of cores rather than clock frequency to deliver increased computing performance.These many core systems can be combined to bult as distributed computing system known as High Performance Computing (HPC). HPC is the most powerful and largest scale computing systems enables researchers to study systems that would otherwise be impractical, or impossible, to investigate in the real world due to their complexity. Consequently, fast solver algorithms of the next generation need to be amenable to parallelization or HPC and implemented with appropriate load-balancing, synchronization and cache utilization.Efficient parallelization of CEM methods with the heterogionus/homogenious distributed system is still a challenge.
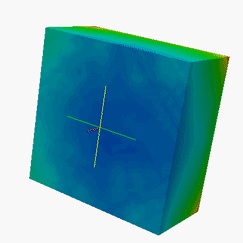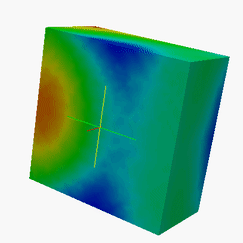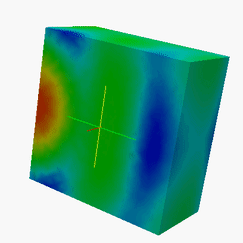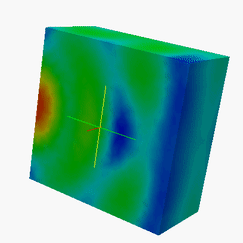
Examples of H-Matrix solutions:Current flow over and inside lossless dilelectric cube and conducting sphere from 100 MHz to 600MHz.